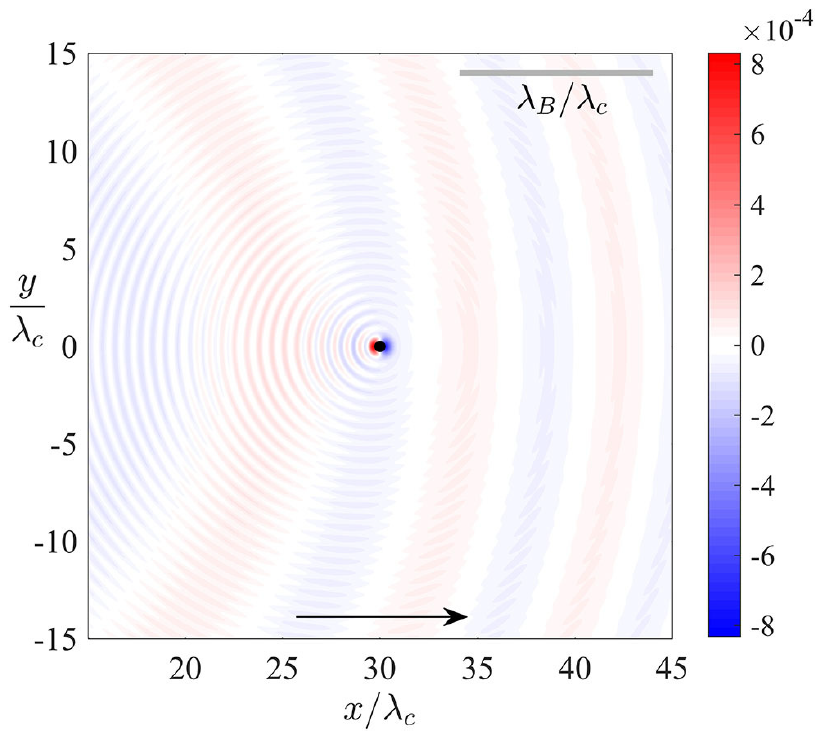
We consider the hydrodynamic quantum field theory proposed by Dagan and Bush (2020), a model of quantum dynamics inspired by Louis de Broglie and informed by the hydrodynamic pilot-wave system discovered by Couder and Fort. According to this theory, a quantum particle has an internal vibration at twice the Compton frequency that generates disturbances in an ambient scalar field, the result being self-propulsion of the particle through a resonant interaction with its pilot-wave field. Particular attention is given here to providing theoretical rationale for the geometric form of the wave field generated by steady, rectilinear particle motion at a prescribed speed, where signatures of both the de Broglie and Compton wavelengths are generally evident. While focus is given to the one-dimensional geometry considered by Dagan and Bush, we also deduce the form of the pilot wave in two dimensions. We further consider the influence on the pilot-wave form of the details of the particle-induced wave generation, specifically the spatial extent and vibration frequency of the particle. Finally, guided by analogous theoretical descriptions of the hydrodynamic system, we recast the particle dynamics in terms of an integro-differential trajectory equation. Analysis of this equation in the non-relativistic limit reveals a critical wave-particle coupling parameter, above which the particle self-propels. Our results provide the foundation for subsequent theoretical investigations of hydrodynamic quantum field theory, including the stability analysis of various dynamical states.
See paper: Durey, M. and Bush, J.W.M., Frontiers in Physics (2020).
