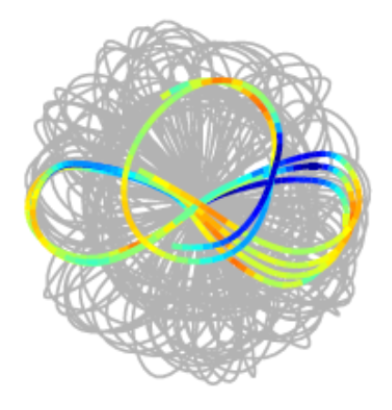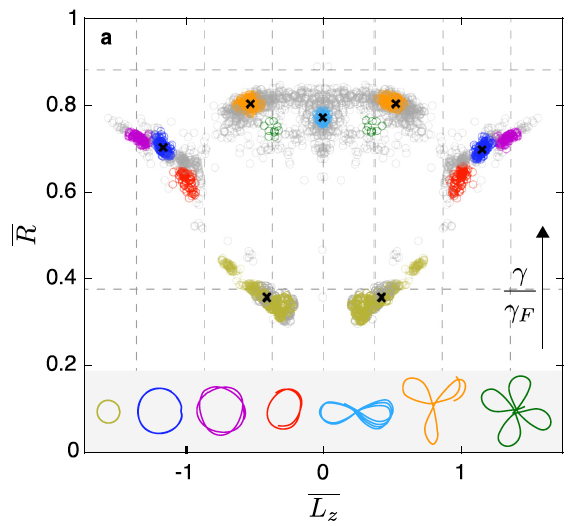
A millimetric liquid droplet may walk across the surface of a vibrating liquid bath through a resonant interaction with its self-generated wavefield. Such walking droplets, or “walkers,” have attracted considerable recent interest because they exhibit certain features previously believed to be exclusive to the microscopic, quantum realm. In particular, the intricate motion of a walker confined to a closed geometry is known to give rise to a coherent wave-like statistical behavior similar to that of electrons confined to quantum corrals. Here, we examine experimentally the dynamics of a walker inside a circular corral. We first illustrate the emergence of a variety of stable dynamical states for relatively low vibrational accelerations, which lead to a double quantisation in angular momentum and orbital radius. We then characterise the system’s transition to chaos for increasing vibrational acceleration and illustrate the resulting breakdown of the double quantisation. Finally, we discuss the similarities and differences between the dynamics and statistics of a walker inside a circular corral and that of a walker subject to a simple harmonic potential.
See paper: Cristea-Platon, T., Sáenz, P.J. and Bush, J.W.M., Chaos, 2018.