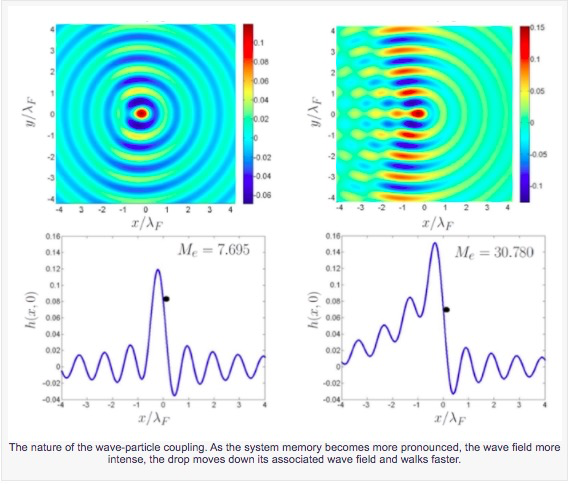
We present the results of a theoretical investigation of droplets bouncing on a vertically vibrating fluid bath. An integro-differential equation for the horizontal motion of the drop is developed by approximating the drop as a continuous moving source of standing waves. We demonstrate that, as the forcing acceleration is increased, the bouncing state destabilizes into steady horizontal motion along a straight line, a walking state, via a supercritical pitchfork bifurcation. Predictions for the dependence of the walking threshold and drop speed on the system parameters compare favorably with experimental data. By considering the stability of the walking state, we show that the drop is stable to perturbations in the direction of motion and neutrally stable to lateral perturbations. This result lends insight into the possibility of chaotic dynamics emerging when droplets walk in complex geometries.
See paper: Oza, Rosales & Bush (2013).
