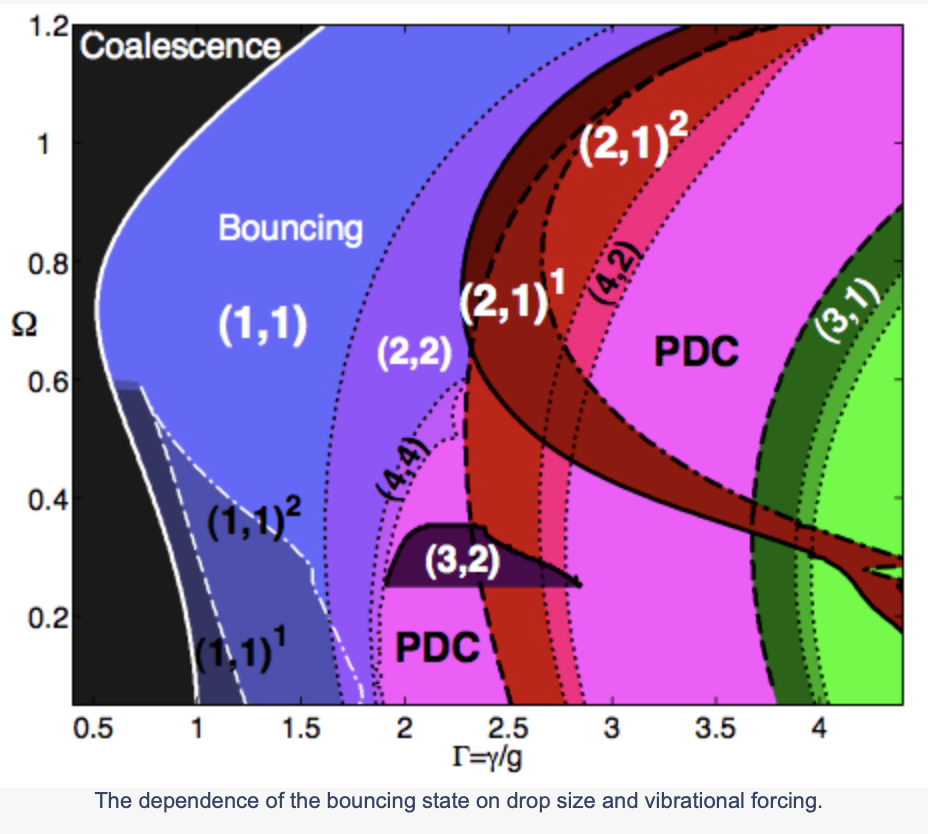
We present the results of a combined experimental and theoretical investigation of millimetric droplets bouncing on a vertically vibrating fluid bath. We first characterize the system experimentally, deducing the dependence of the droplet dynamics on the system parameters, specifically, the drop size, driving acceleration and driving frequency. As the acceleration is increased, depending on drop size, we observe the transition from coalescing to hovering or bouncing states, then period-doubling events that may culminate in either walking drops or chaotic bouncing states. The drop’s vertical dynamics depends critically on the ratio of the driving frequency to the drop’s natural oscillation frequency. For example, when the data describing the coalescence-bouncing threshold and period-doubling thresholds are described in terms of this ratio, they collapse onto a single curve. We observe and rationalize the coexistence of two non-coalescing states, bouncing and hovering, for identical system parameters. In the former state the contact time is prescribed by the drop dynamics; in the latter, by the driving frequency. The bouncing states are described by theoretical models of increasing complexity whose predictions are tested against data. We first model the drop-bath interaction in terms of a linear spring, then develop a logarithmic spring model that better captures the drop dynamics over a wider range of parameter space. While the linear spring model provides a faster, less accurate option, the logarithmic spring model is found to be more accurate and consistent with all existing data.
See paper: Molacek & Bush (2013).
