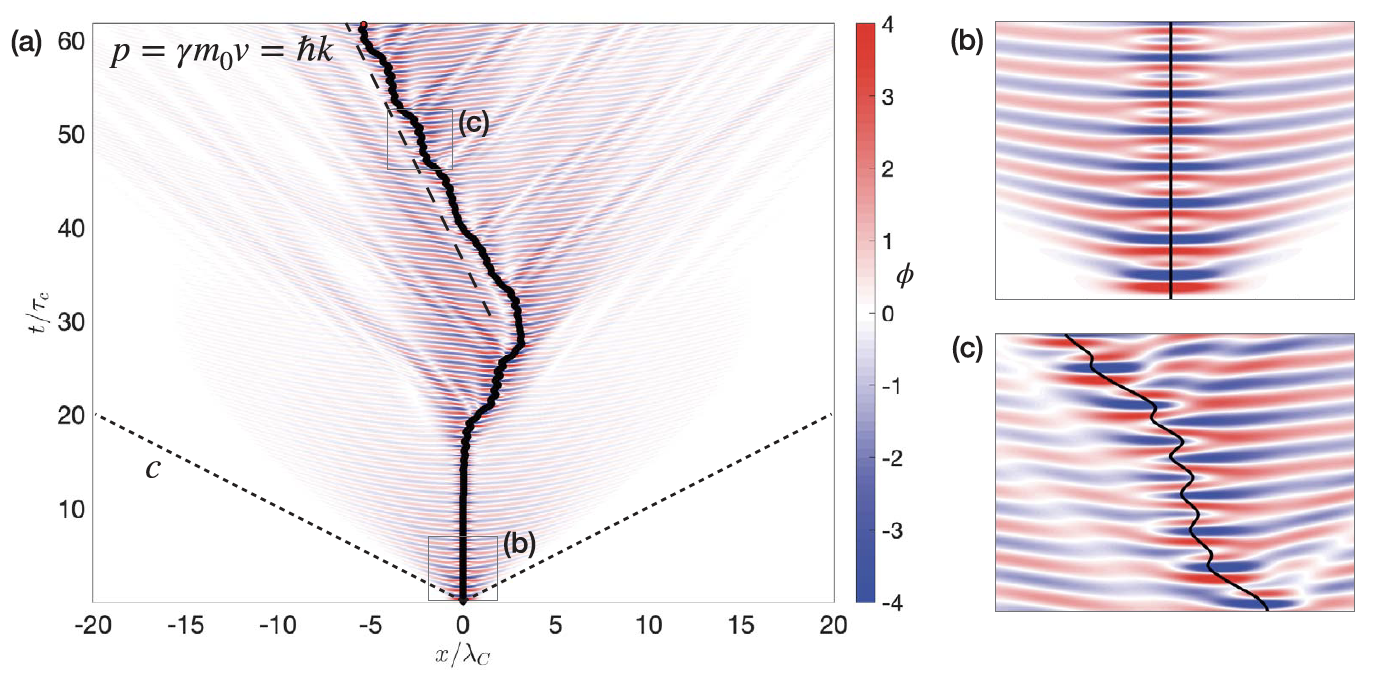
We revisit de Broglie’s double-solution pilot-wave theory in light of insights gained from the hydrodynamic pilot-wave system discovered by Couder and Fort (2005). De Broglie proposed that quantum particles are characterized by an internal oscillation at the Compton frequency, at which rest mass energy is exchanged with field energy. He further proposed that the resulting pilot-wave field satisfies the Klein–Gordon equation. While he developed a guidance equation for the particle, he did not specify how the particle generates the wave. Informed by the hydrodynamic pilot-wave system, we explore a variant of de Broglie’s mechanics in which the form of the Compton-scale dynamic interaction between particle and pilot wave is specified. The particle is modeled as a localized periodic disturbance of the Klein–Gordon field at twice the Compton frequency. We simulate the evolution of the particle position by assuming that the particle is propelled by the local gradient of its pilot wave field. Resonance is achieved between the particle and its pilot wave, leading to self-excited motion of the particle. The particle locks into quasi-steady motion characterized by a mean momentum p= hbar * k, where k is the wavenumber of the surrounding matter waves. Speed modulations along the particle path arise with the de Broglie wavelength and frequency ck. The emergent dynamics is strongly reminiscent of that arising in the hydrodynamic pilot-wave system, on the basis of which we anticipate the emergence of quantum statistics in various settings. Our results suggest the potential value of a new hydrodynamically-inspired pilot-wave theory for the motion of quantum particles.
See paper: Dagan, Y. and Bush, J.W.M., Comptes Rendus Mécanique (2020).