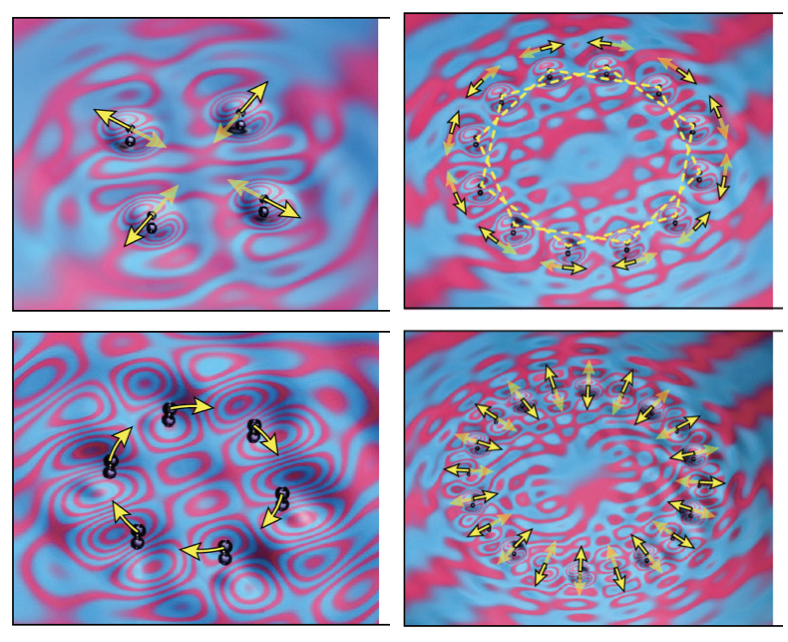
We present the results of a combined experimental and theoretical investigation of the stability of rings of millimetric droplets bouncing on the surface of a vibrating liquid bath. As the bath’s vibrational acceleration is increased progressively, droplet rings are found to destabilize into a rich variety of dynamical states including steady rotational motion, periodic radial or azimuthal oscillations and azimuthal travelling waves. The instability observed is dependent on the ring’s initial radius and drop number, and whether the drops are bouncing in- or out-of-phase relative to their neighbours. As the vibrational acceleration is further increased, more exotic dynamics emerges, including quasi-periodic motion and rearrangement into regular polygonal structures. Linear stability analysis and simulation of the rings rationalize the observed behaviour. We demonstrate that the wave amplitude beneath each drop has a significant influence on the stability of the multi-droplet structures: the system seeks to minimize the mean wave amplitude beneath the drops at impact. Our work provides insight into the complex interactions and collective motions that arise in bouncing-droplet aggregates.
