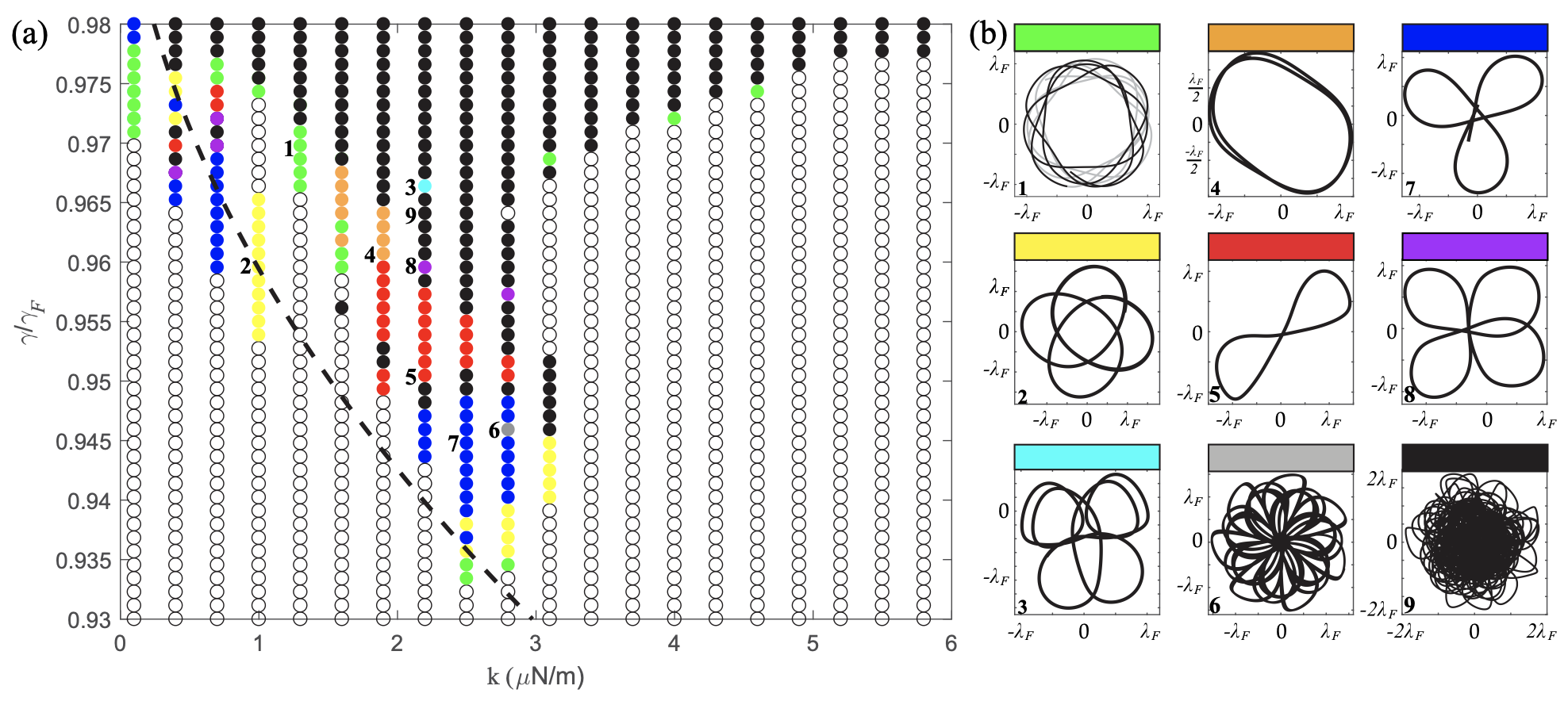
We present the results of a numerical investigation of droplets walking in a harmonic potential on a vibrating fluid bath. The droplet’s trajectory is described by an integro-differential equation, which is simulated numerically in various parameter regimes. We produce a regime diagram that summarizes the dependence of the walker’s behavior on the system parameters for a droplet of fixed size. At relatively low vibrational forcing, a number of periodic and quasiperiodic trajectories emerge. In the limit of large vibrational forcing, the walker’s trajectory becomes chaotic, but the resulting trajectories can be decomposed into portions of unstable quasiperiodic states.
See paper: Kurianski, K.M., Oza, A.U. and Bush, J.W.M., Physical Review Fluids (2017).