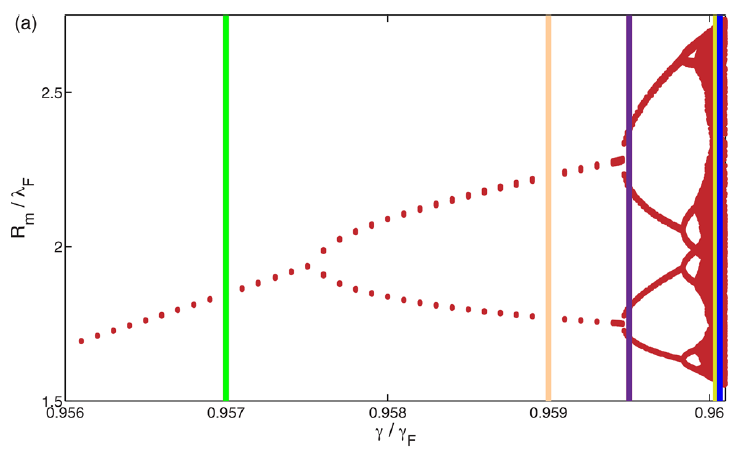
We present the results of a numerical investigation of the emergence of chaos in the orbital dynamics of droplets walking on a vertically vibrating fluid bath and acted upon by one of the three different external forces, specifically, Coriolis, Coulomb, or linear spring forces. As the vibrational forcing of the bath is increased progressively, circular orbits destabilize into wobbling orbits and eventually chaotic trajectories. We demonstrate that the route to chaos depends on the form of the external force. When acted upon by Coriolis or Coulomb forces, the droplet’s orbital motion becomes chaotic through a period-doubling cascade. In the presence of a central harmonic potential, the transition to chaos follows a path reminiscent of the Ruelle-Takens-Newhouse scenario.
See paper: Tambasco, L.D., Harris, D.M., Oza, A.U., Rosales, R.R. and Bush, J.W.M., Chaos (2016).
