The circular hydraulic jump may arise when a fluid jet falling vertically at high Reynolds number strikes a horizontal plate. Fluid is expelled radially, and the layer generally thins until reaching a critical radius at which the layer depth increases abruptly. Predictions for the jump radius based on inviscid theory were presented by Rayleigh (1914). The dominant influence of fluid viscosity on the jump radius was elucidated by Watson (1964), who developed an appropriate description of the boundary layer that develops from the lower boundary. We have elucidated the influence of surface tension on the circular hydraulic jump, both its size ( Bush & Aristoff, JFM 2003 ) and stability ( Bush, Aristoff & Hosoi, JFM 2006 ), through combined theoretical and experimental investigations.
Circular Jumps and Crowns
Figures 1 and 2 illustrate the laminar circular hydraulic jump, and Figure 3 shows a turbulent circular jump with a pronounced outer crown.
The polygonal regime
Elegaard et al. (1998, 1999) first demonstrated that the axisymmetry of the viscous hydraulic jump may be broken, resulting in steady polygonal jumps. We have further examined these striking flow structures.
The clover regime
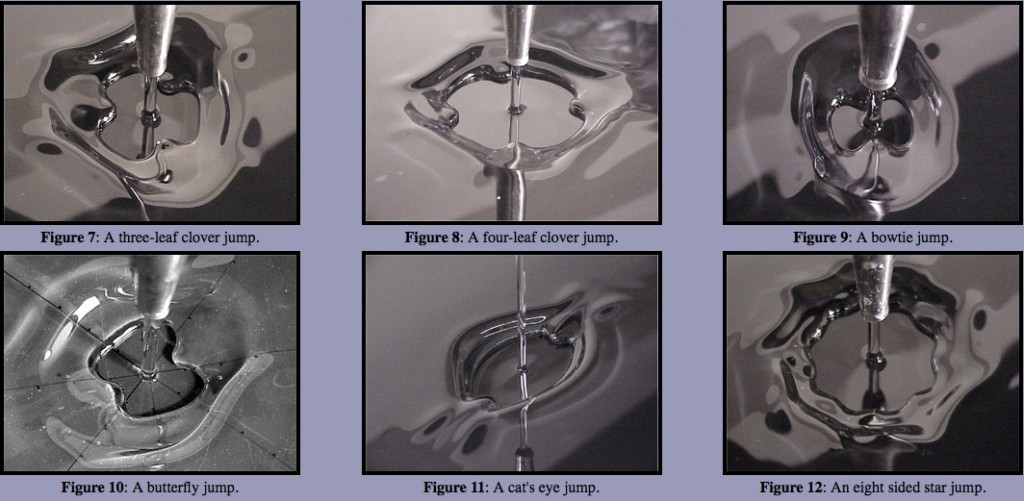
In addition to the polygonal forms, we have discovered a new class of steady asymmetric jumps that include structures resembling cat’s eyes, three and four-leaf clovers, bowties and butterflies (Figures 7-12). We have conducted a parameter study that reveals the dependence of the jump structure on the governing parameters. We acknowledge Jeff Leblanc for his assistance with our study.
References
Bush, J.W.M. & Aristoff, J.M., 2003. The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229-238. (Linked above.)
Bush, J.W.M., Aristoff, J.M., Hosoi, A.E., 2006. An experimental investigation of the stability of the circular hydraulic jump. J. Fluid Mech. 558, 33-52. (Linked above)
Ellegaard, C, Hansen, A.E., Haaning, A., Marcussen, A., Bohr, T., Hansen, J.L. and Watanabe, S., 1998. Creating corners in kitchen sink flows. Nature, 392, 767-768.
Ellegaard, C, Hansen, A.E., Haaning, A., Hansen, K., Marcussen, A., Bohr, T., Hansen, J.L. and Watanabe, S., 1999. Polygonal hydraulic jumps. Nonlinearity, 12, 1-7.
Rayleigh, L., 1914. On the theory of long waves and bores. Proc. Roy. Soc. Lond. A. 90, 324.
Watson, E.J., 1964. The spread of a liquid jet over a horizontal plane. J. Fluid Mech. 20, 481-499.